


Boy's Surface is an immersion of the real projective plane, RP2, in
R3. It was constructed by Werner Boy, working under
David Hilbert, in 1901. It is continuous and has threefold symmetry,
self-intersecting at a triple point. The Boy's Surface shown here is
parametrized by three homogeneous polynomials of degree four which are
defined on the sphere, S2. These polynomials are:
F = Sqrt(3)/2 [(y2 - z2) (x2 +
y2 + z2) + zx (z2 - x2) +
xy (y2 - x2)]
G = 1/2 [(2x2 - y2 - z2) (x2 +
y2 + z2) + 2yz (y2 - z2) +
zx (x2 - z2) + xy (y2 - x2)]
H = 1/8 (x + y + z) [(x + y + z)3 + 4 (y - x) (z - y) (x - z)]
where
x = 0.577295 Cos(s) - 0.577295 Cos(t) Sin(s) - 0.3950426 Sin(s) Sin(t)
y = 0.577295 Cos(s) + 0.577295 Cos(t) Sin(s) - 0.333365 Sin(s) Sin(t)
z = 0.57746 Cos(s) + 0.728199 Sin(s) Sin(t)
s ranges from 0 to Pi/2 and t ranges from 0 to 2 Pi
(Note: If your browser is configured to run .oogl files in Geomview, you can click on the links below the pictures to interact with the surfaces using Geomview.)
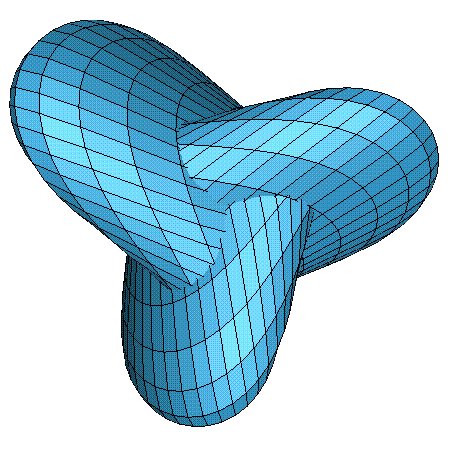
This cut-away view shows the triple point from the inside:

This animation shows the level curves of a Boy's Surface that has
been tricolored to emphasize the threefold symmetry:
(Note: If you are viewing this page with Internet Explorer on a Mac,
the following animation may not run properly. )

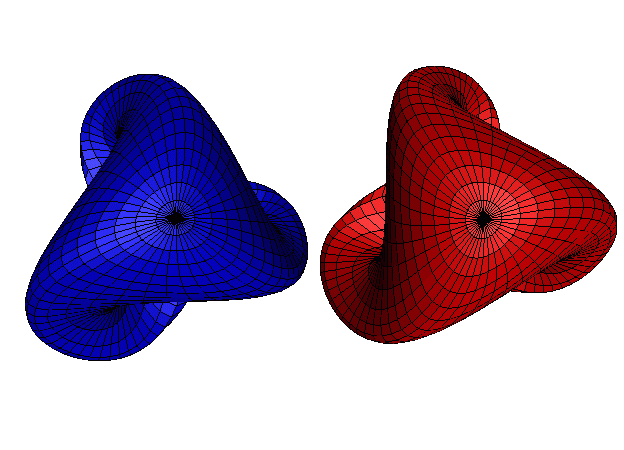
The picture below is a comparison of a direct Boy's Surface
versus an inverse Boy's Surface. The direct Boy's Surface is the one
on the right, whose legs curl down and clockwise. The inverse Boy's
Surface, shown on the left, has legs that curl down and
counterclockwise.
See these surfaces in Geomview
See a Boy's Surface mesh in Geomview
(This file takes a relatively long time to load.)
Other pages:
What is the
real projective plane?
Boy's Surface has many other
parametrizations besides the one shown in the pictures above.
Learn more. . .
We have written a few programs that create emodules
in Geomview. All of these programs allow you to interact with Boy's Surface and should help you to become more familiar with it.
Links about Boy's Surface.
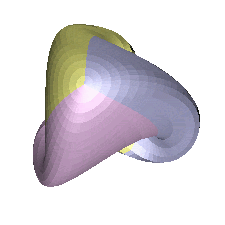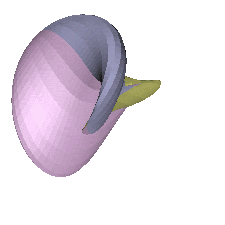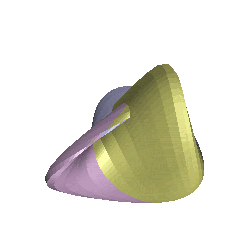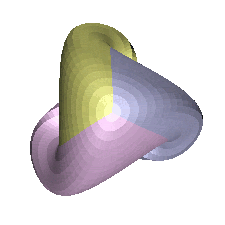
Sources:
"Models of the Real Projective Plane" by F. Apery, Chapter 2
The animate GIFs were put together with The GIMP
The pictures on this page were made with Mathematica and Geomview
E-mail us:
Amy Hawthorne
Jenny Posson-Brown