F. Apery defines a Boy's Surface as the real zero set of the
degree six polynomial
F. Apery defines a Boy's Surface as the real zero set of the
degree six polynomial
p(x,y,z) = 64 (1 - z)3 z3 - 48 (1 -
z)2 z2 (3x2 + 3y2 +
2z2) + 12 (1 - z) z (27 (x2 +
y2)2 - 24 z2 (x2 +
y2) + 36 Sqrt(2) y z (y2 - 3 x2) +
4z4) + (9x2 + 9y2 - 2z2)
(-81 (x2 + y2)2 - 72 z2
(x2 + y2) + 108 Sqrt(2) x z (x2 -
3y2) + 4z4)
which can be described by
f = Cos(s) (1 - Sqrt(2) Sin(s) Cos(s) Sin(3t))-1
[(Sqrt(2)/3) Cos(s) Cos(2t) + (2/3) Sin(s) Cos(t)]
g = Cos(s) (1 - Sqrt(2) Sin(s) Cos(s) Sin(3t))-1
[(Sqrt(2)/3) Cos(s) Sin(2t) - (2/3) Sin(s) Sin(t)]
h = Cos(s) (1 - Sqrt(2) Sin(s) Cos(s) Sin(3t))-1 [Cos(s)]
s and t both range from 0 to Pi
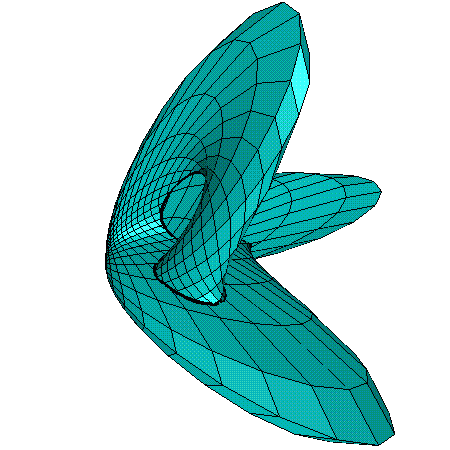
f = 2 (3 - Cos(6t))-1 [(2/3) Sin(Pi/4 - 3t) Cos(t)]
g = 2 (3 - Cos(6t))-1 [(2/3) Sin(Pi/4 - 3t) Sin(t)]
h = 2 (3 - Cos(6t))-1 [1]
The following parametrization was found by Petit and Souriau in 1981.
However, it has not been proven to be a Boy's Surface.
a = 10 + 1.41 Sin(6t - Pi/3) + 1.98 Sin(3t - Pi/6)
b = 10 + 1.41 Sin(6t - Pi/3) - 1.98 Sin(3t - Pi/6)
c = a2 - b2
d = (a2 + b2)1/2
e = (Pi/8) Sin(3t)
f = c/d + a Cos(u) - Sin(u)
g = d + a Cos(u) + b Sin(u)
x = 3.3 (f Cos(t) - g Sin(e) Sin(t))
y = 3.3 (f Sin(t) + g Sin(e) Cos(t))
z = 4 (g Cos(e) - 10)
t ranges from 0 to Pi and u ranges from 0 to 2 Pi
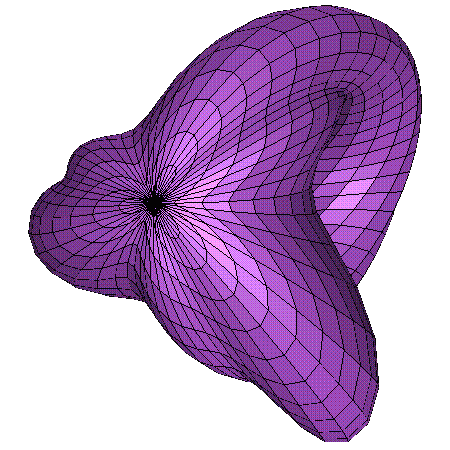
This parametrization by R. Bryant uses the representation of
P2 as the unit circle on the complex plane where the
mapping is invariante under z -> -1/(complex conjugate of z).
x = (g12 + g22 + g32)-1 g1
y = (g12 + g22 + g32)-1 g2
z = (g12 + g22 + g32)-1 g3
where
g1 = -(3/2) Im[z (1 - z4) (z6 + Sqrt(5)
z3 - 1)-1]
g2 = -(3/2) Re[z (1 + z4) (z6 + Sqrt(5)
z3 - 1)-1]
g3 = -1/2 + Im[(1 + z6) (z6 + Sqrt(5)
z3 - 1)-1]
and
z = r Cos(t) + i r Sin(t)
r ranges from 0 to 1 and t ranges from 0 to 2 Pi
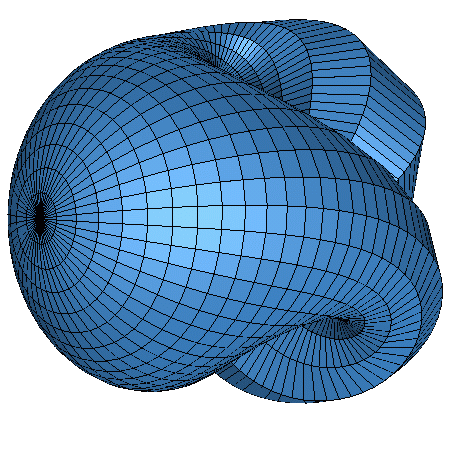
See a mesh of this surface in Geomview
This parametrization by J. F. Hughes consists of three homogeneous
polynomials of degree eight, defined on S2:
